MINIMOS CUADRADOS
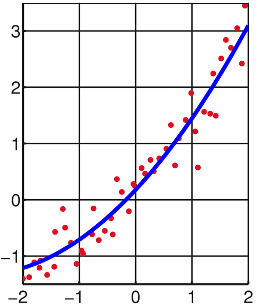
Es una técnica de Anàlisis numerico encuadrada dentro de la optimización matemática,
en la que, dados un conjunto de pares (o ternas, etc), se intenta encontrar la función que mejor se aproxime a los datos (un
"mejor ajuste"), de acuerdo con el criterio de mínimo error
cuadrático.
En su forma más simple, intenta
minimizar la suma de
cuadrados de las diferencias ordenadas (llamadas residuos) entre los
puntos generados por la función y los correspondientes en los datos.
Específicamente, se llama mínimos
cuadrados promedio (LMS) cuando el número de datos medidos es
1 y se usa el método de descenso por gradiente
para minimizar el residuo cuadrado. Se puede demostrar que LMS minimiza el
residuo cuadrado esperado, con el mínimo de operaciones (por iteración), pero
requiere un gran número de iteraciones para converger.
Desde un punto de vista
estadístico, un requisito implícito para que funcione el método de mínimos
cuadrados es que los errores de cada medida estén distribuidos de forma
aleatoria. El teorema de Gauss-Márkov prueba que los
estimadores mínimos cuadráticos carecen de sesgo y que el muestreo de datos no
tiene que ajustarse, por ejemplo, a una distribución normal. También es importante que
los datos recogidos estén bien escogidos, para que permitan visibilidad en las
variables que han de ser resueltas.
La técnica de mínimos cuadrados
se usa comúnmente en el ajuste de curvas. Muchos otros problemas de optimización
pueden expresarse también en forma de mínimos cuadrados, minimizando la energía
o maximizando la entropía.


